Order of operations can be frustrating to teach, but it doesn’t have to be. There’s no question that this is an extremely challenging topic for elementary students. Fortunately, there are loads of strategies for teaching order of operations that are both fun and effective.
One reason kids struggle with this concept is that there are so many rules to learn and follow. Even worse, rules that appear to be simple often prove to be deceptively complex.
For example, most kids can easily remember that multiplication and division are always performed before addition and subtraction, especially after they learn to follow the order described by “PEMDAS.”
However, they tend to get stuck when an equation includes both multiplication AND division. Most kids automatically multiply before dividing, but order of operations tells us to perform the operation that comes first when reading the problem from left to right. No wonder kids find order of operations to be super confusing!
Another reason kids struggle is that even when they understand how to use order of operations correctly, they don’t apply the rules systematically. Because the problems look easy, students try to rely on mental math alone to solve them. This may work with the easy problems, but mental math isn’t effective with more complex problems that include multiple operations, parentheses, exponents.
After watching my students struggle with order of operations, I developed a simple lesson that worked every time. As a result, my students actually remembered the rules and could easily apply them to any problem. I’d like to share these no-fail strategies with you, along with two free order of operations printables you can use to help your students grasp these concepts.
Order of Operations Lesson
The lesson begins with a quick activity to get students thinking about why we need rules for solving equations. This lesson “hook” is followed by an order of operations mini-lesson, a guided practice session, and a fast-paced game that doubles as a formative assessment activity.
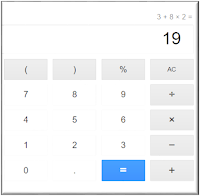
To get the most from the activities, each student will need a dry erase board or tablet where they can work out the problems. You’ll also need at least one calculator for the class that uses order of operations correctly. A physical calculator is fine if displayed under a document camera, or you can use an online calculator. Be sure to test the calculator prior to the lesson to be sure it can handle order of operations problems. To find out, enter 1 + 2 x 3 and press the = sign. The correct answer is 7, so if your calculator displays 9 as the answer, it does NOT use order of operations correctly.
1. Lesson Hook: Solve a Not-so-simple Equation  Â
Before you teach PEMDAS or any other strategy, challenge your students to solve a simple equation such as this one: 3 + 8 x 2 = ? Ask your students to write the equation on a dry erase board or tablet, and then solve it and show you the answer.
You’re likely to see two different answers, but resist the urge to reveal the correct answer at this point. Most students will say the answer is 22 because they added 3 and 8 and then multiplied the sum by 2. However, who have studied order of operations in the past will say the answer is 19 because they multiplied 8 times 2 and added 3 to the product. Your students might be a bit confused when they notice that some of their classmates have different answers, but they are about to become even more confused!
Tell your students that you’re going to use a calculator to check the answer, and as they watch, enter the problem above. When the calculator displays 19 as the answer, act surprised and say you must have entered the problem wrong. Enter it carefully again, and when you get the same answer, try a different calculator. When you get the same answer yet again, ask your students to pair up with a partner to discuss why the calculator keeps giving the “wrong” answer. After they talk it over for a few minutes, tell them that 19 is actually the correct answer, and that you’re going to teach them some important rules for solving problems that involve more than one operation.
This activity is a great way to start your order of operations lesson because it creates a feeling of “cognitive dissonance,” a state of mind in which we struggle to assimilate new facts that don’t match what we thought we knew about a topic. When students experience cognitive dissonance, they become eager to learn and open to new ideas, so it’s the perfect time to start the actual instruction.
2. Direct Instruction: Introduce Order of Operations
How you introduce order of operations will depend on your students’ readiness and their prior experiences with algebraic concepts. You might want to start by teaching your students how to use parentheses to indicate which part of an equation should be solved first. Write an equation two different ways, keeping the numbers the same but placing the parentheses around different pairs of numbers like this: (5Â + 3) x 2 = ? and 5 + (3 x 2) = ?
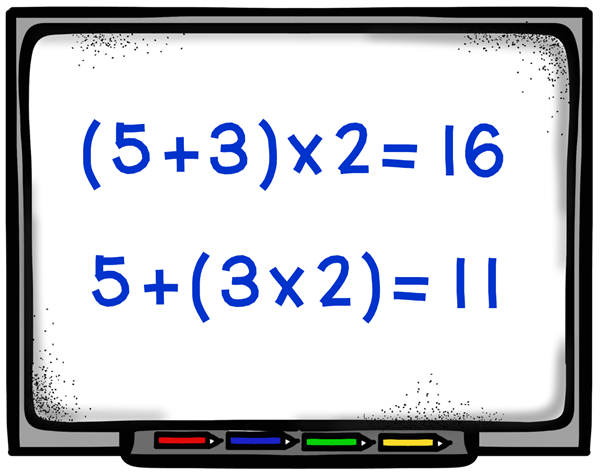
Show your students how to solve both problems, and point out that even though the numbers used in the equations are the same, the solutions are different. Give your students several more pairs of problems that have the same numbers and the parentheses in different locations. Stop after each problem to discuss the solution and clear up misunderstandings.
Next, display an equation that doesn’t have parentheses, like 15 – 5 x 2 = x. Point out that it’s not clear which part of the problem should be solved first, and as they’ve seen with the previous example, the order in which you perform the operations DOES matter.
Tell your students that mathematicians have agreed upon a set of rules called the “order of operations” that must be followed when solving problems. If your students have already studied exponents, you can teach the acronym PEMDAS which stands for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. The phrase “Please Excuse My Dear Aunt Sally” will help them remember the order of those letters. If your students haven’t studied exponents, you can substitute the acronym PMDAS and the phrase “Pass My Dad a Sandwich.”
3. Guided Practice: Teaching the Step-by-Step Method for Solving Problems
For the next part of the lesson, you’ll need to download the Order of Operations Freebie shown above. This freebie consists of three pages from Order of Operations Bingo Level 1. Exponents are not mentioned on these pages, and the acronym PMDAS is used instead of PEMDAS.
After using the Order of Operations Review to explain the PMDAS acronym, display a copy of the practice page or give each student a paper copy. Introduce the step-by-step method for evaluating algebraic expressions by explaining the example at the top of the page. Using this strategy, each step is written on a separate line.
Guide your students through the process of solving the 6 practice problems one at a time. Check and discuss the solutions after each problem, and be sure to have them show you their work. If needed, refer to the answer key on page 3Â of the freebie for step-by-step solutions.
If you have not taught this step-by step-method of solving order of operations problems, you might be tempted to skip it and let your students use mental math. Most of the problems are so easy that your students may be able to solve them without writing out each step.
However, relying on mental math to solve more challenging problems results in a lot of careless mistakes, so I recommending teaching your students to follow this step-by-step strategy with EVERY problem. If they get in the habit of using this systematic approach, they will be able to solve more complex problems with ease later. Trust me on this!
4. Play an Order of Operations Game
After your students understand how to solve order of operations problems, they’ll need lots of practice while the concepts are fresh in their minds. Games are far more effective for practice than worksheets because they are fast-pace and fun, motivating students to solve dozens of problems in a short time.
If you play the game as a class and discuss the answers after each problem, your students will know within a few round of the game if they are solving the problems correctly. If they aren’t, they will be motivated to ask questions and seek help to improve. Furthermore, many games can serve as formative assessment activities if you walk around while students are solving each problem to observe their work. Without having to administer a formal test, you’ll be able to see who understands the concepts and who needs more help.
Order of Operations Bingo is my favorite activity for practicing this skill because players can’t win without using order of operations correctly. To foster math skill development, ask your students to work out each problem on a dry erase board or tablet, using the step-by-step method. Stop after each problem to discuss each solution before presenting the next task card. Remind your students that they can only cover the answer on their Bingo boards with a chip if they had the correct answer BEFORE you revealed the solution to the class. If you enforce this rule, I can guarantee a huge drop in careless errors after the first round of the game!
5. Review and Practice with Order of Operations Task Cards or digital Boom Cards Â
The first four strategies are extremely effective for teaching kids how to use order of operations correctly. However, in order to retain what they’ve learned, your students will need opportunities for more review and practice throughout the year.
Whether you’re teaching students remotely or in the classroom, the Order of Operations Boom Cards below will meet this need perfectly! Boom Cards are self-checking, interactive, digital task cards that can be played on almost any device with Internet access. They are hosted on the Boom Learning platform, but free accounts are available. My Boom Cards also include optional audio directions; students can click the sound icon in the corner of each card to hear the words on the card read aloud! Kids love these interactive task cards because they’re fun, and teachers love them because they’re so effective!
If your students enjoy escape-room style activities, they will love the new Order of Operations Escape Room Zoo Adventures! Both sets begin with a scenario that requires the player to visit 5 animal exhibits and the solve order of operations math problems they find there. After they solve them correctly, they will be given the secret number codes that are needed to unlock a padlock. My daughter Amy and I had so much fun creating these Boom Cards, and they are perfect for students who enjoy a challenge or who need a little extra practice.
As with my other Order of Operations products, there are two levels of difficulty in both the practice Boom Cards and the Escape Room Boom Cards. Both Order of Operations Level 1 products include some problems with parentheses, but none of them have exponents. The Order of Operations Level 2 Boom Cards are more challenging because most cards have parentheses and/or exponents.
If you prefer printable task cards, the Order of Operations Task Cards below will make it easy for your students keep these skills fresh. You can use the task cards shown below in math centers and with cooperative learning activities like Showdown or Team Scoot.
Differentiating Instruction is Easy
Differentiating instruction is easy because there are two levels of instructional materials, including the task cards, bingo game, and assessments. Level 1 includes basic problems like the ones used in the freebie. The materials for Level 2 have more complex problems and some of the problems include exponents. Both sets of bingo games, the printable task cards, and the assessments are included in one cost-saving bundle. If your curriculum includes exponents, the Order of Operations Games and Tests Bundle is your best option. If you use both levels in your classroom, you might want to print the task cards and game materials for each level on different colored card stock to keep them separate. (Boom Cards must be purchased separately.)
Classroom-Tested: Teacher and Student Approved
I love having teachers field test my products with their students. Several teachers tested Order of Operations Bingo with their students, and two of them sent pictures of their students playing the game. I love to see photos of kids using my lessons and activities, and I couldn’t resist sharing a few of them with you!
Fourth grade teacher Christina Ashburn tested Order of Operations Bingo and had her students solve the problems on dry erase boards as described in the lesson. She didn’t have bingo chips, so she laminated the game boards and had her students color over the answers with dry erase markers. I honestly never thought of doing that, but it’s a brilliant idea! For one thing, if kids are solving problems on dry erase boards, their markers should be handy. Also, you don’t have to worry about plastic Bingo chips ending up all over the classroom floor!
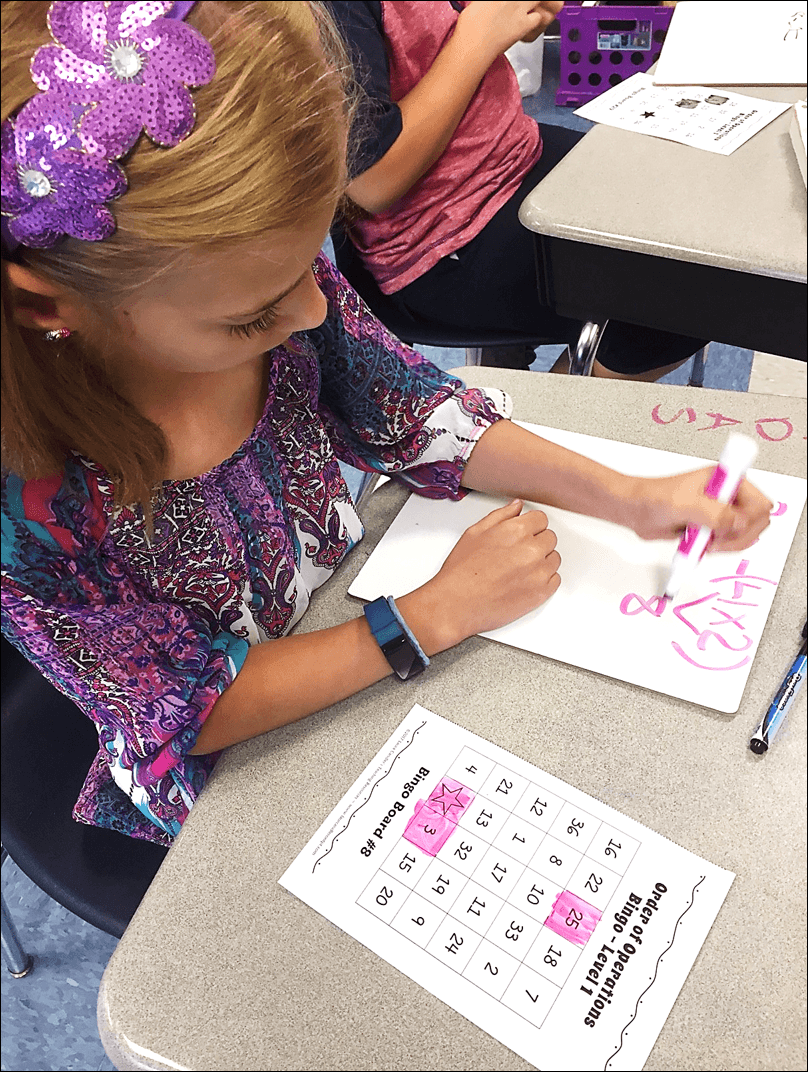
Fifth grade teacher Sheryl Nicholas also tested the game in her class. After observing her students play Order of Operations Bingo, she discovered an unexpected benefit. Sheryl explained, “My favorite part was how my non-English speakers immediately felt involved in the review. So much lately is ‘drill and test,’ but this made it a lot more interesting for the students. All were engaged in the activity and there was quite a bit of math talk as well as individual practicing of skills.”
After they played the game, Sheryl interviewed her students to get their feedback and shared some of their comments with me. I especially loved reading two comments about having to write out the steps of each problem. One student said, “I liked that you wouldn’t let me do them in my head but made me write the problems on the iPad and do them.” Another student wasn’t quite as enthusiastic about that part of the lesson, stating, “I wish you would have let me do these problems in my head. But then again, I always work too fast so I probably did better since I had to write them down.”
I just laughed when I read that last comment because it’s exactly the sort of thing some of my students would have said! This “no-fail” order of operations lesson is fun for students, and the step-by-step strategies make it highly effective, too. After playing the game, even kids recognize the importance of writing out the steps when solving order of operations problems, whether they like it or not!
